| Definitions | Realizer, t  T, Knd, Top, T, Knd, Top,   x. t(x), x. t(x),  x:A. B(x), a:A fp x:A. B(x), a:A fp B(a), Type, B(a), Type,  x.A(x), R-da(R;i), x:A x.A(x), R-da(R;i), x:A  B(x), KindDeq, P B(x), KindDeq, P   Q, f(x), Void, lnk(k), source(l), f(x)?z, destination(l), Id, s = t, isrcv(k), Q, f(x), Void, lnk(k), source(l), f(x)?z, destination(l), Id, s = t, isrcv(k),  b, x b, x  dom(f), R-has-loc(R;i), IdLnk, rcv(l,tg), Prop, P dom(f), R-has-loc(R;i), IdLnk, rcv(l,tg), Prop, P   Q, P & Q, P Q, P & Q, P   Q, Q,  x x dom(f). v=f(x) dom(f). v=f(x)   P(x;v), R-interface(A;B), {T}, SQType(T), s ~ t, left+right, Atom$n, tag(k), False, P(x;v), R-interface(A;B), {T}, SQType(T), s ~ t, left+right, Atom$n, tag(k), False,  A, A,   b, b,  , x:A , x:A B(x), Unit, EqDecider(T), B(x), Unit, EqDecider(T), 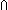 x:A. B(x), rec(x.A(x)), if b x:A. B(x), rec(x.A(x)), if b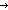 t else f fi, Case b of inl(x) t else f fi, Case b of inl(x)  s(x) ; inr(y) s(x) ; inr(y)  t(y), f(a), lnk_rcv{lnk_rcv_compseq_tag_def:ObjectId}(tg; l), True, isrcv_rcv{isrcv_rcv_compseq_tag_def:ObjectId}(tg; l), P t(y), f(a), lnk_rcv{lnk_rcv_compseq_tag_def:ObjectId}(tg; l), True, isrcv_rcv{isrcv_rcv_compseq_tag_def:ObjectId}(tg; l), P  Q, Dec(P) Q, Dec(P) |